LNF
Users Site

SCIENTIFIC CASE

SIDDHARTA-2 — The scientific case

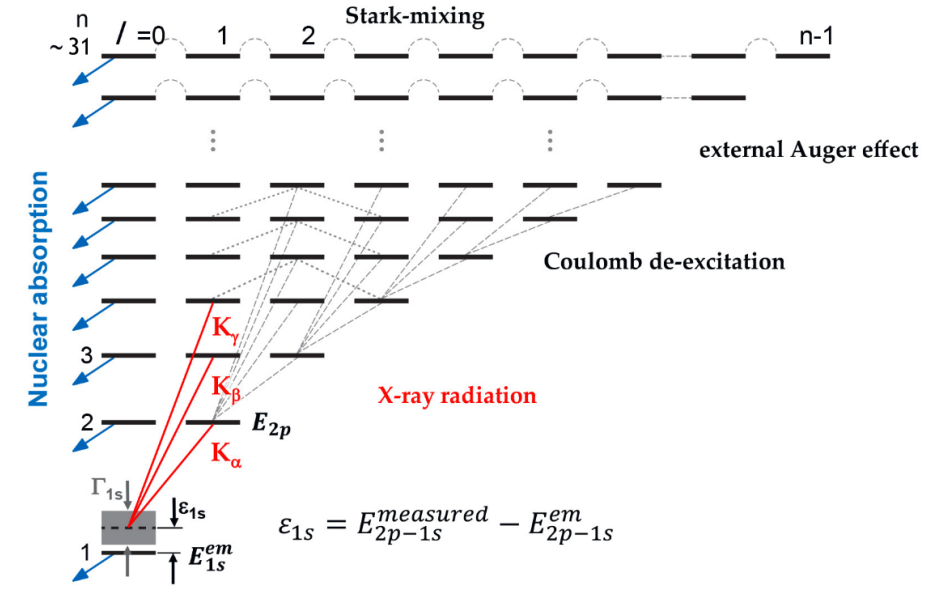
Kaons are mesons: particles consisting of quark-antiquark pairs. In the specific, kaons contain the strange quark (s). Kaonic atoms are atomic systems in which a negatively charged kaon (K–) replaces an electron in the atomic shell.  Whenever a K– enters in a target, it is slowed down by loosing its kinetic energy through the interaction with the medium and can be captured by an atom, via the electromagnetic interaction with the nucleus. The K– is captured in a highly excited atomic level, which depends on the reduced mass of the system. After capture, the K– starts an elettromagnetic cascade process towards the more internal atomic levels. The cascade ends with the nuclear absorption of the K–. During the cascade process, the K– could reach the innermost atomic level, where the strong interaction between the kaon and the nucleus adds up to the electromagnetic one, producing a detectable shift and broadening of the energy level that can be extracted with dedicated x-ray spectroscopy measurement [1].

     

 

Kaonic atoms allow the investigation of the K–-N interaction in the low-energy limit, the so called non-perturbative regime, hardly achievable by scattering experiments due to the strong coupling to πΣ  channel and the presence of the Λ(1405) resonance just below threshold [2,3]. In kaonic atoms, the K–-N intercation occurs at negligible momentum transfer, nearly “at threshold”, thus avoiding the extrapolation at zero energy as for the scattering experiments. The x-ray spectroscopy measurements of the strong interaction induced shift and width of the 1s level in kaonic hydrogen (K–-H) and kaonic deuterium (K–-d) provide information on the relationship between spontaneous and explicit chiral symmetry breaking in Quantum ChromoDynamics (QCD). In the specific, it allows to extract the kaon-proton and kaon-deuterium scattering lengths using the Deser–Truemann-type formula with isospin-breaking corrections [4, 5]:

$\varepsilon ^{H} _{1s}+\dfrac{i}{2}\Gamma ^{H} _{1s}=2\alpha ^{3}\mu ^{2} _{\bar{K}p} a_{\bar{K}p}(1-2\alpha \mu ^{2} _{\bar{K}p} (\ln \alpha -1)a_{\bar{K}p})$

$\varepsilon ^{D} _{1s}+\dfrac{i}{2}\Gamma ^{D} _{1s}=2\alpha ^{3}\mu ^{2} _{\bar{K}d} a_{\bar{K}d}(1-2\alpha \mu ^{2} _{\bar{K}d} (\ln \alpha -1)a_{\bar{K}d})$

 

In the formulas above, $a_{\bar{K}p}$ and $a_{\bar{K}p}$ are the $\bar{K}p$ and $\bar{K}d$ scattering lenghts ($K^{-}$ is also indicated as $\bar{K}$), $\mu _{\bar{K}p}$ and $\mu _{\bar{K}d}$ are the reduced masses of $\bar{K}p$ and $\bar{K}d$ systems, $\varepsilon ^{H} _{1s}$, $\varepsilon ^{D} _{1s}$ and $\Gamma ^{H} _{1s}$, $\Gamma ^{D} _{1s}$ are, respectively, the energy shifts and widths of 1s level in kaonic hydrogen and kaonic deuterium, and $\alpha$ is the fine-structure constant [8].
Kaon proton ($\bar{K}p$) and kaon neutron ($\bar{K}n$) isospin-dependent lenghts can be extracted by the Deser–Truemann-type formula, with the following result:

$a_{\bar{K}p}=\dfrac{1}{2}(a_{0}+a_{1})$

$a_{\bar{K}n}=a_{1}$

$a_{\bar{K}d}=\dfrac{k}{4}(a_{0}+3a_{1})+C=\dfrac{k}{2}(a_{0}+a_{1})+C$

In the formulas above, $a_{0}$ and $a_{1}$ are the isospin-dependent lenghts (I=0,1), $k=\dfrac{4(m_{N}+m_{K})}{2m_{N}+m_{K}}$ with $m_{N}$ and $m_{K}$ respecively nucleon and kaon masses, and C is a term including all higher orders [8].

 
 

Scheme of the K– electromagnetic cascade in the atomic shell. Further details in [6,7].

 
 

The SIDDHARTA-2 experiment aims to measure the 2p ⇒ 1s x-ray transition in K–-d with the Silicon Drift Detectors (SDDs), to extract the strong interaction induced shift and width of the 1s energy level, due to the strong K–-N interaction [8,9]. The most precise measurement of the strong interaction induced shift and width in K–-H was performed by the SIDDHARTA experiment in 2009 [10]. Measuring K–-d, the SIDDHARTA collaboration will provide the values of kaon-proton and kaon-neutron scattering lenghts in the low energy limit, for the first time. These values will be fundamental constraints for the models which aims to describe QCD interaction at low energies in the strangeness framework.

 

References